斯坦福凸优化课程Video2.4_
本文共 348 字，大约阅读时间需要 1 分钟。
title: 斯坦福凸优化课程Video2-4
tags: note notebook: 6- 英文课程-14-convex optimization ---斯坦福凸优化课程Video2-4
超平面分离理论
如果两个集合是可分离的凸集那么可以满足下面的条件。
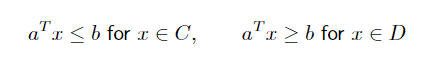
在这个条件下，我们画出的图像是这样的：
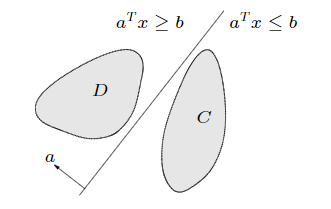
可以看到，如上图所示的，如果可以用一条直线，超平面，将两个集合划分开来，那么称两个集合为可分离集合。
也同时可以称，直线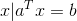
可以分离C和D。
支持超平面原理
支持超平面是满足方程
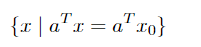的x0是集合c的边界点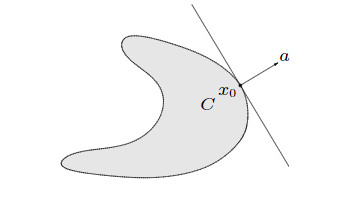 
如果c是凸的，那么在所有的c的边界点都存在支持超平面。
双锥和广泛不等式
我们先看双锥的定义，双锥是满足如下方程的等式
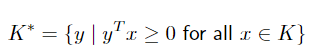
我们看这幅图，如果我们有一个锥k和一个向量y，那么那么对于我们的向量y的锥
转载地址：http://nxasx.baihongyu.com/
你可能感兴趣的文章
promise
查看>>
将Java应用部署到SAP云平台neo环境的两种方式
查看>>
==与equal的区别
查看>>
数据批量导入Oracle数据库
查看>>
调用lumisoft组件发邮件 不需要身份验证 不需要密码
查看>>
DW 正则
查看>>
抓屏原理
查看>>
ASP.NET Web API自身对CORS的支持: EnableCorsAttribute特性背后的故事
查看>>
UNIX网络编程读书笔记:TCP输出、UDP输出和SCTP输出
查看>>
扩展 DbUtility （1）
查看>>
iOS开发UI篇—使用picker View控件完成一个简单的选餐应用
查看>>
Apple Developer Registration and DUNS Number Not Accepted
查看>>
Hadoop学习笔记系列文章导航
查看>>
Win7 64位 php-5.5.13+Apache 2.4.9+mysql-5.6.19 配置
查看>>
不同页面之间实现参数传递的几种方式讨论
查看>>
程序员进阶之路—如何独当一面
查看>>
SpringMVC中ModelAndView addObject()设置的值jsp取不到的问题
查看>>
Prometheus : 入门
查看>>
使用 PowerShell 创建和修改 ExpressRoute 线路
查看>>
PHP如何学习？
查看>>